为什么需要复杂度分析

衡量算法的优劣，有两种评估方式：事前估计和后期测试。

后期测试有性能测试、基准测试（Benchmark）等手段。

但是，后期测试有以下限制：

• 测试结果非常依赖测试环境。如：不同机型、不同编译器版本、不同硬件配置等等，都会影响测试结果。
• 测试结果受数据规模的影响很大。

所以，需要一种方法，可以不受环境或数据规模的影响，粗略地估计算法的执行效率。这种方法就是复杂度分析。

时间复杂度分析

什么是 LSM 树

LSM 树具有以下 3 个特点：

1. 将索引分为内存和磁盘两部分，并在内存达到阈值时启动树合并（Merge Trees）；
2. 用批量写入代替随机写入，并且用预写日志 WAL 技术（Write AheadLog，预写日志技术）保证内存数据，在系统崩溃后可以被恢复；
3. 数据采取类似日志追加写的方式写入（Log Structured）磁盘，以顺序写的方式提高写
   入效率。

LSM 树的这些特点，使得它相对于 B+ 树，在写入性能上有大幅提升。所以，许多 NoSQL 系统都使用 LSM 树作为检索引擎，而且还对 LSM 树进行了优化以提升检索性能。

什么是 B+树

B+树是在二叉查找树的基础上进行了改造：树中的节点并不存储数据本身，而是只是作为索引。每个叶子节点串在一条链表上，链表中的数据是从小到大有序的。

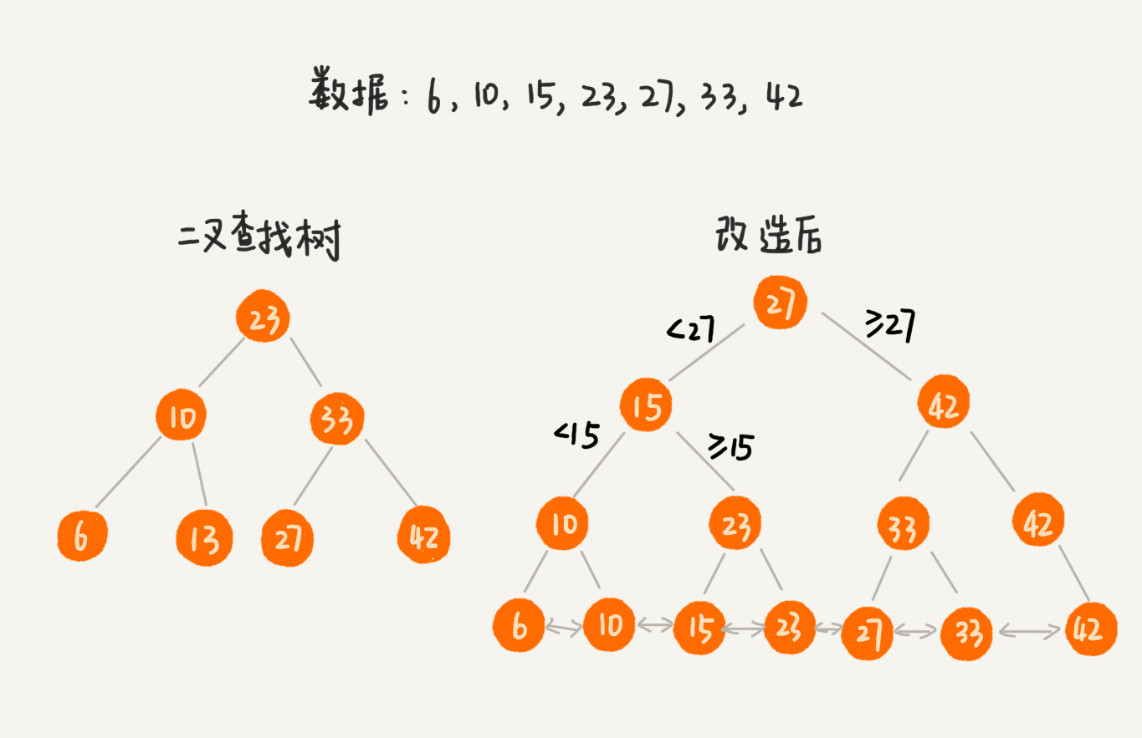
改造之后，如果我们要求某个区间的数据。我们只需要拿区间的起始值，在树中进行查找，当查找到某个叶子节点之后，我们再顺着链表往后遍历，直到链表中的结点数据值大于区间的终止值为止。所有遍历到的数据，就是符合区间值的所有数据。

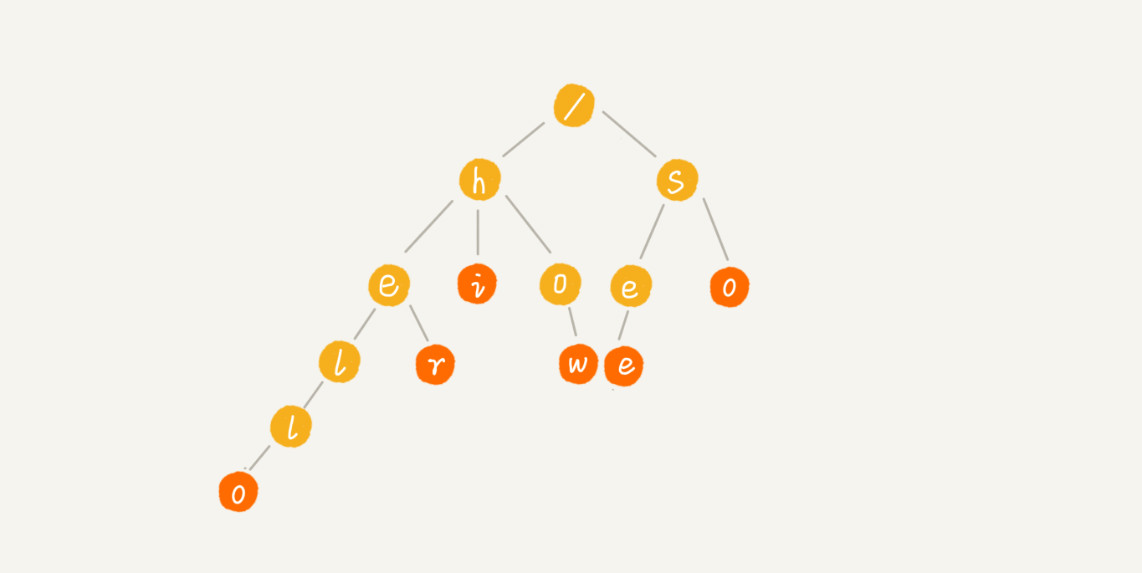
什么是字典树

Trie 树（又叫“前缀树”或“字典树”）是一种用于快速查询“某个字符串/字符前缀”是否存在的数据结构。

• 根节点（Root）不包含字符，除根节点外的每一个节点都仅包含一个字符；
• 从根节点到某一节点路径上所经过的字符连接起来，即为该节点对应的字符串；
• 任意节点的所有子节点所包含的字符都不相同；

什么是跳表

对于一个有序数组，可以使用高效的二分查找法，其时间复杂度为 O(log n)。

但是，即使是有序的链表，也只能使用低效的顺序查找，其时间复杂度为 O(n)。

平衡二叉树

平衡二叉树的严格定义是这样的：二叉树中任意一个节点的左右子树的高度相差不能大于 1。

完全二叉树、满二叉树其实都是平衡二叉树，但是非完全二叉树也有可能是平衡二叉树。

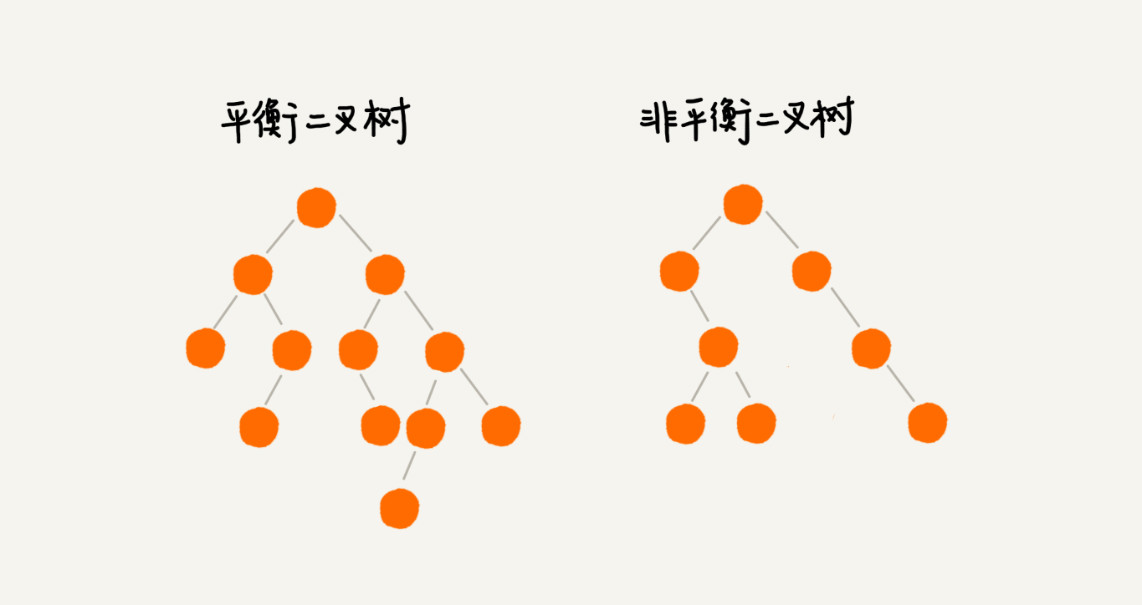
平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”、比较“平衡”，不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。

数组和链表分别代表了连续空间和不连续空间的存储方式，它们是线性表（Linear List）的典型代表。其他所有的数据结构，比如栈、队列、二叉树、B+ 树等，实际上都是这两者的结合和变化。

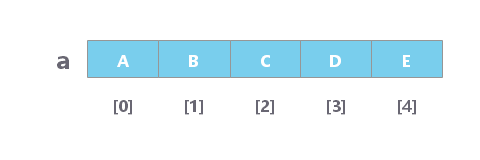
数组

数组用 连续 的内存空间来存储数据。

数组的访问

数组元素的访问是以行或列索引的单一下标表示。

在计算机科学中，一个图就是一些顶点的集合，这些顶点通过一系列边结对（连接）。顶点用圆圈表示，边就是这些圆圈之间的连线。顶点之间通过边连接。

什么是图

• 阶（Order） - 图 G 中点集 V 的大小称作图 G 的阶。
• 子图（Sub-Graph） - 当图 G'=(V',E')其中 V‘包含于 V，E’包含于 E，则 G'称作图 G=(V,E)的子图。每个图都是本身的子图。
• 生成子图（Spanning Sub-Graph） - 指满足条件 V(G') = V(G)的 G 的子图 G'。
• 导出子图（Induced Subgraph） - 以图 G 的顶点集 V 的非空子集V1 为顶点集，以两端点均在 V1 中的全体边为边集的 G 的子图，称为 V1 导出的导出子图；以图 G 的边集 E 的非空子集 E1 为边集，以 E1 中边关联的顶点的全体为顶点集的 G 的子图，称为 E1 导出的导出子图。
• 有向图 - 如果给图的每条边规定一个方向，那么得到的图称为有向图。
• 无向图 - 边没有方向的图称为无向图。
• 度（Degree） - 一个顶点的度是指与该顶点相关联的边的条数，顶点 v 的度记作 d(v)。
• 入度（In-degree）和出度（Out-degree） - 对于有向图来说，一个顶点的度可细分为入度和出度。一个顶点的入度是指与其关联的各边之中，以其为终点的边数；出度则是相对的概念，指以该顶点为起点的边数。
• 自环（Loop） - 若一条边的两个顶点为同一顶点，则此边称作自环。
• 路径（Path） - 从 u 到 v 的一条路径是指一个序列 v0,e1,v1,e2,v2,...ek,vk，其中 ei 的顶点为 vi 及 vi - 1，k 称作路径的长度。如果它的起止顶点相同，该路径是“闭”的，反之，则称为“开”的。一条路径称为一简单路径(simple path)，如果路径中除起始与终止顶点可以重合外，所有顶点两两不等。
• 行迹（Trace） - 如果路径 P(u,v)中的边各不相同，则该路径称为 u 到 v 的一条行迹。闭的行迹称作回路（Circuit）。
• 轨迹（Track） - 如果路径 P(u,v)中的顶点各不相同，则该路径称为 u 到 v 的一条轨迹。闭的轨迹称作圈（Cycle）。
• 桥（Bridge） - 若去掉一条边，便会使得整个图不连通，该边称为桥。

哈希表 是一种使用 哈希函数 组织数据，以支持快速插入和搜索的数据结构。

有两种不同类型的哈希表：哈希集合 和 哈希映射。

• 哈希集合 是集合数据结构的实现之一，用于存储非重复值。
• 哈希映射 是映射 数据结构的实现之一，用于存储(key, value)键值对。